
We develop some preliminary di erential geometry in order to state and prove the Gauss-Bonnet theorem, which relates a compact surface’s Gaussian curvature to its Euler characteristic. For comparison, it is not strictly true that surface areas can be treated in this way. THE GAUSS-BONNET THEOREM KAREN BUTT Abstract. We could argue on physical grounds that no real-world measurement of the flux can depend on the granular structure of \(S\) at arbitrarily small scales, but this feels a little unsatisfying. The difficulty arises because a smooth shape typically cannot be built out of bricks, a fact that is well known to Lego enthusiasts who build elaborate models of the Death Star. Gausss Law is a general law applying to any closed surface.

The electric flux through an area is defined as the electric field multiplied by the area of the surface projected in a plane perpendicular to the field. How is electric flux related to Gauss law When we talk about the relation between electric flux and Gauss law, the law states that the net electric flux in a closed surface will be zero if the volume that is defined by the surface contains a net charge. No matter which choices of coordinates or frame elds are used tocompute it, the Gaussian Curvature is the same function. The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. Gauss theorem is helpful for finding a field when there is a certain symmetry as it tells us how the field is directed. Let S 1 and S 2 be the bottom and top faces, respectively, and let S 3 be the lateral face. Theorem (GausssTheorema Egregium, 1826) Gauss Curvature is an invariant of the Riemannan metric on.
#Gauss theorem curved space how to#
If \(R\) could be dissected exactly into boxes, then this would complete the proof, since the sum of exterior contributions would be the same as the flux through \(S\), and the left-hand side of Gauss’s theorem would be additive over the boxes, as is the right-hand side. theorem really just says how to compute a line integral' of a gradient along a compact curve in Euclidean space. theorem Gauss’ theorem Calculating volume Gauss’ theorem Example Let F be the radial vector eld xi+yj+zk and let Dthe be solid cylinder of radius aand height bwith axis on the z-axis and faces at z 0 and z b. We show that the RVB method can easily be employed to compute the Hawking temperature of black holes having spherically symmetric topology. Notice that the posterior is non-Gaussian and unimodal, as expected. If we have a data set Das shown in Figure 3.1(b) then this induces a posterior distribution in weight space as shown in Figure 3.1(c). Contours of the prior p(w) are illustrated in Figure 3.1(a).
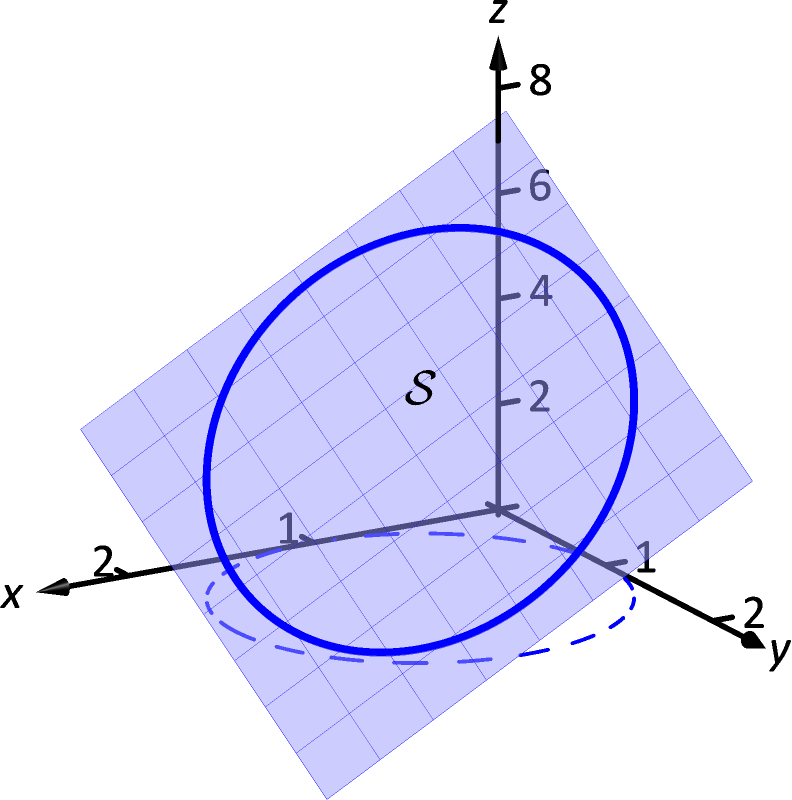
Therefore if we add up the fluxes through the surfaces of all the boxes, the contributions on the interior cancel, and we’re left with only the exterior contributions. In this paper, we apply the recently found topological method of Robson, Villari and Biancalana (RVB) 1, 2 to the various black holes to derive their Hawking temperature. The prior in weight space is Gaussian and for simplicity we have set p I. Where the faces of two boxes coincide on the interior of \(R\), their own outward directions are opposite.


 0 kommentar(er)
0 kommentar(er)
